三行定律概率分析
1. 概述
最近,虎牙直播 狼人杀主播 大申屠007 提出了一套 网杀理论:“三行定律,麻吕模型”,该理论可大致描述为:
在一局
12人的标准场狼人杀(网杀)局里,四个狼人的分布大概率会出现在其中的某三行中,其中不出现三行中的概率大约是10.30303030...%。
由于是与著名 麻省理工学院 数学家 吕学士 联合研制而成,故也称“三行定律,麻吕模型”。
(ren)纯(zhen)属(ni)娱(jiu)乐(shu)一(le)下 ![]()
![]()
![]()
示例如下:
图中,狼人分别为:3, 6, 8, 12 号玩家,其中 8 号在第二行, 3 号在第三行, 6, 12 号则在第六行,一共三行。
2. 分布概率
下面我们来分析一下狼人分布的概率。
2.1. 位置分组
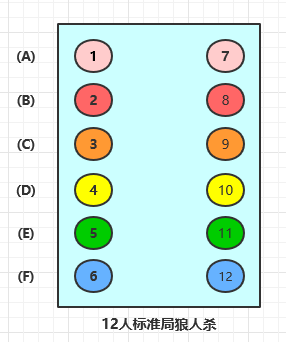
为了便于讨论,我们把 1 到 12 号玩家分为 6 组,分别为 A, B, C, D, E, F 共六行,如下图所示:
2.2. 分布类型
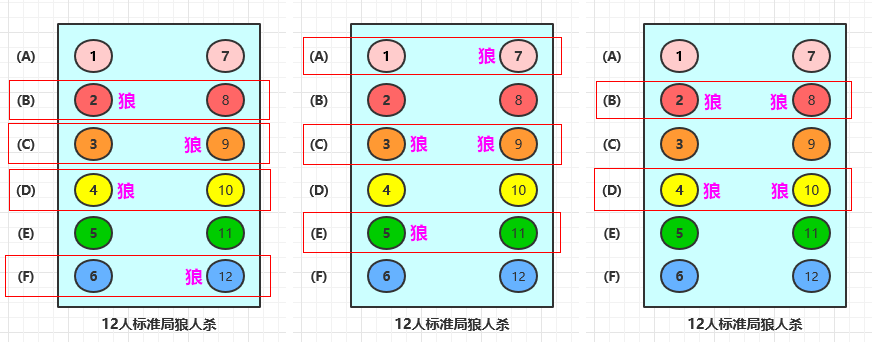
我们可以想象一下,四个狼人随机分布到 12 个位置中,分布最均匀的时候,可能会分布到了不同的 4 行中;如果分布得稍微差一点,可能会有两个狼人会被分到同一行中,那么狼人总共就分布在 3 行里;分布的最不均匀的时候,就是四个狼人分别分布在不同的两行里面,所以总共有且只有 3 种不同的类型,即:
- 四个狼人分布不在不同的
4行内; - 四个狼人分布不在不同的
3行内; - 四个狼人分布不在不同的
2行内;
如下图所示:
2.3. 概率分析
下面分别分析一下这三种不同类型出现的概率,我们先从最简单的四狼分布在两行中开始分析。
先分析一下,四个狼人随机分发到 12 个位置中的所有可能的总数,根据排列组合的知识,这个值等于 \(C_{12}^4\) ,即:
\(C_{12}^4 = (12 * 11 * 10 * 9) / (4 * 3 * 2 * 1) = 495\) 种可能。
2.3.1. 2-2 类型
四狼分布在两行中的图示如下:
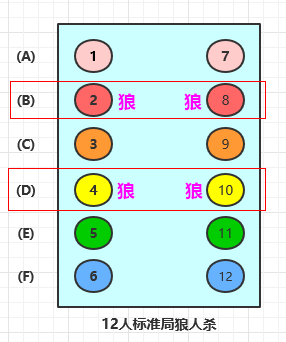
上图中,可以看到,无论狼分布在哪两行里,都可以把它视为 2-2 分布,所以我们把这种类型称为 2-2 类型,这样便于分析概率。
下面来分析一下概率,首先,从 A, B, C, D, E, F 共 6 行中任选两行出来,一共有 \(C_6^2 = (6 * 5) / (2 * 1) = 15\) 种可能。
当选出了这任意两行后,例如上图中的 B, D 两行,再考虑把所有狼人放进这两行中。
由于在每一行中,例如 B 行中,共有 2, 8 两个号码,且这两个号码是不分先后的,所以把两只狼放到行 B 中的可能性有且只有一种,即 2, 8 双狼。同样的道理,把两只狼放到行 D 中也有且只有一种可能性。
所以,四狼分布在任意两行中总的可能分布情况一共有:
\(C_6^2 * 1 * 1 = 15 * 1 * 1 = 15\) 种可能。
所以“2-2 类型”出现的概率是:\(P = 15 / 495 = 3.03030 \%\)。
2.3.2. 1-2-1 类型
四狼分布在三行中的图示如下:
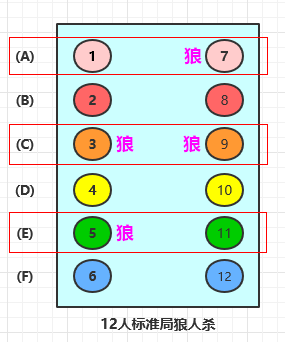
上图中,可以看到,狼分布在任意三行里,可能的分布格式有 2-1-1, 1-2-1, 1-1-2 三种可能,为了方便讨论,我们把这种类型统称为 1-2-1 类型 。
分析一下这种类型的概率,首先,从 A, B, C, D, E, F 共 6 行中任选三行出来,一共有 \(C_6^3 = (6 * 5 * 4) / (3 * 2 * 1) = 20\) 种可能。
当我们选出了这任意三行后,比如上图中的 A, C, E 三行,再考虑把四个狼人放进这三行中。
我们先考虑 “1-2-1 类型” 中的 2,即 C 这一行,跟前面 “2-2” 类型类似,这种情况没有选择,有且只一种可能性。但是从上往下看,这个 2 可能是这三行中靠最前的,或是中间的,又或是靠最后的,例如上图中,这个 2 就是靠中间的,也就是 1-2-1 这种类型。在前面我们也分析过了,分布的格式一共有 2-1-1, 1-2-1, 1-1-2 三种不同可能,所以这个 2 的可能共有 \(3 * 1 = 3\) 种可能;
再来看 “1-2-1” 中的另外两个 “1”,例如:第一行 A,此时,狼人可能是 1 或者 7,所以一共有两种可能的情况。对于第五行 E,同理,狼人可能是 5 或者 11,同样也是两种可能。所以,选出任意 3 行后,再把四个狼人放到这 3 行内,一共有 \(3 * 2 * 2 = 12\) 种不同可能。
综上可得,四狼分布在任意三行中总的可能分布情况一共有:
\(C_6^3 * 3 * 2 * 2 = 20 * 12 = 240\) 种可能。
所以“1-2-1 类型”出现的概率是:\(P = 240 / 495 = 48.4848 \%\)。
2.3.3. 1-1-1-1 类型
四狼分布在四行中的图示如下:
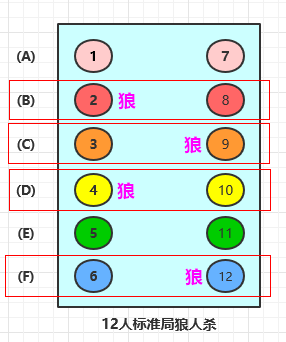
上图中,可以看到,狼分布在任意四行里,为了方便讨论,我们把这种类型统称为 1-1-1-1 类型 。
分析一下这种类型的概率,首先,从 A, B, C, D, E, F 共 6 行中任选四行出来,一共有 \(C_6^4 = C_6^2 = (6 * 5) / (2 * 1) = 15\) 种可能。
当我们选出了这任意四行后,比如上图中的 B, C, D, F 四行,再考虑把四个狼人放进这四行中。
这种情况比较简单,对于被选出来的每一行,都有两个位置可选,也就是每一行都有两种可能,比如第二行 B,可选 2 或者 8。所以,选出任意 4 行后,再把四个狼人放到这 4 行内,一共有 \(2 * 2 * 2 * 2 = 16\) 种不同可能。
综上可得,四狼分布在任意四行中总的可能分布情况一共有:
\(C_6^4 * 2 * 2 * 2 * 2 = 15 * 16 = 240\) 种可能。
所以“1-1-1-1 类型”出现的概率是:\(P = 240 / 495 = 48.4848 \%\)。
3. 简单验证
把以上三种类型的可能情况的总数合计一下,可以得到总数为:
\(15 + 240 + 240 = 495\),这和我们前面得到 4 个狼人随机分配到 12 个位置的所有可能总数 \(C_{12}^4 = 495\) 是相等的,说明所有的情况我们都考虑到了,结果是正确的。
4. 后记
上面的分析其实是有一点小瑕疵的,我也是后来才想到的,道理也很简单,我会另写一篇文章讨论,有兴趣的朋友可以先思考一下。
这里给个提示,首先,如果你要找狼人,那么说明你一定是一个好人视角,因为在标准局里,狼人是互相认识的,不需要找狼,对吗?所以,我想聪明的你应该知道问题出在哪了吧……